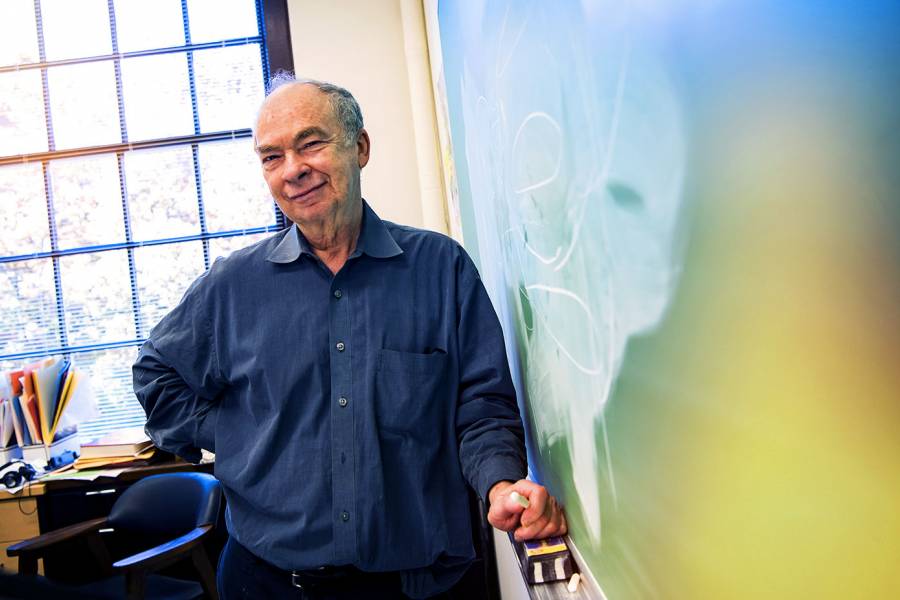Proof of life

In about 900 B.C., the Phoenician princess Dido—overthrown by her ruthless brother—fled to Africa to buy land for herself and her followers. As told in Virgil's Aeneid, King Jarbas offered her as much land as she could enclose with an ox hide.

Clever Dido cut the hide into extremely thin strips. Placing them end to end, and using the Mediterranean Sea as one edge, she formed a circle that was as large as her cord could possibly allow—and plenty big enough for the foundation of what would become the city of Carthage.

"Queen Dido's Problem, as it is known, is at the beginning of many subjects," notes Johns Hopkins mathematician Joel Spruck. From one of the piles of books and papers that blanket his desk in Krieger Hall, all coated in a fine haze of chalk dust, he fetches a book—part mathematical theory, part art tome—titled The Parsimonious Universe, which covers such topics as form and shape, ancient science, and the concept of optimal design. Opening the book to an illustration of Dido's territory, he explains that the problem is related to a host of favorite mathematical puzzles, ranging from where seashells get their shape to the way plants grow to why soap bubbles form the way they do.

"There are many possible shapes, and nature picks the one using the least amount of energy," Spruck says. It follows that the shape that encloses a given area with the smallest possible perimeter is the circle—or, venturing into three dimensions, the sphere.

Simple enough. But things get trickier when you want to generalize this idea beyond circles and spheres to more complicated situations. Recently, Spruck and a colleague took on that challenge and succeeded in proving a long-standing conjecture that the same principle would hold true for other geometries. The proof is an important step for the field of mathematical physics—which goes back to the 17th or 18th century—because it's an issue that connects to many other problems.

"It's at the heart of a great deal of 20th-century math, not just in that field but in related fields," says Spruck, the J.J. Sylvester Professor in the Department of Mathematics at the university's Krieger School of Arts and Sciences.

It's also the latest entry in a succession of proofs for the Cartan-Hadamard conjecture, named after the early-20th-century mathematicians who first posited the idea. Back in 1926, the conjecture was proved for two dimensions. In 1984, it was proved for four dimensions, and for three in 1992. "Then we did all the other dimensions," Spruck says.

Moments after sitting down to explain, Spruck leaps back up—a stick of chalk suddenly appearing in his hand—and begins covering his office chalkboard with equations and curved shapes. The challenge, he explains, was that while the conjecture was relatively straightforward—if you're handy with math—in what's known as Euclidean space, things got more complicated in, say, negatively curved space.

Negatively curved space, Spruck patiently continues, is like a saddle surface instead of a sphere. It includes more area in less space. Think flower petals or coral reefs. The universe might be negatively curved—we don't know for sure.

Negatively curved spaces with no boundaries are called Cartan-Hadamard manifolds, and that is where Spruck and his colleague proved the conjecture in every dimension. They announced their proof with a post on ArXiv (pronounced "archive"), an online, open-access platform where most modern math happens. Many mathematicians check the site daily to stay on top of the latest techniques.

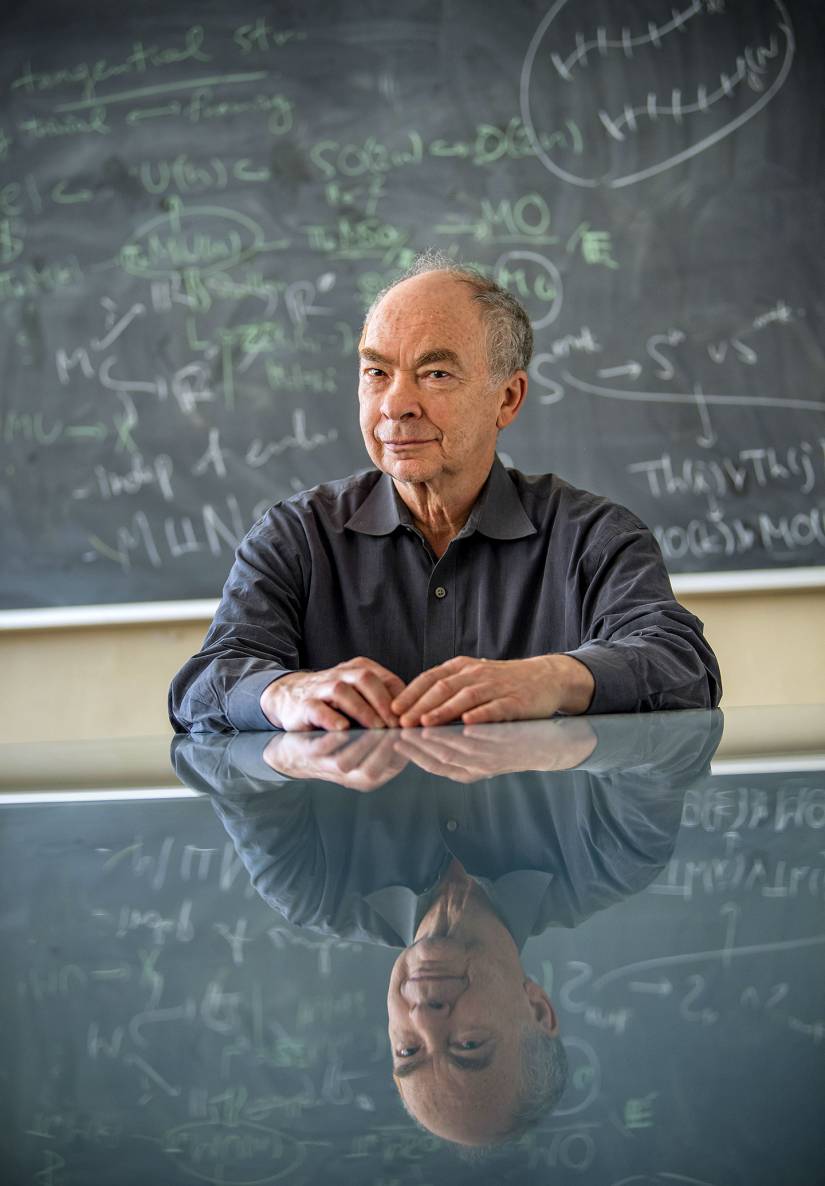
Image credit: Howard Korn / For Johns Hopkins University

The proof filled some 80 pages of text and figures. "It was hard because we had to invent everything; the techniques and stuff, they didn't exist," Spruck says. He'd been curious about the problem for a long time, and invited a former student, Mohammad Ghomi, to tackle it with him. Ghomi, a specialist in classical geometry who received his PhD from Hopkins in 1998, is a professor at Georgia Tech's School of Mathematics. Theirs turned out to be a story of mathematically dramatic rescue from near death.

Spruck had an idea, but he thought it extremely risky and possibly "insane." "Math is all about making your idea concrete: Taking the intuition and making it into something very rigorous," Spruck says. "So we'd try to write up pieces of the plan, but there were conflicting technical problems."

As a year and a half went by, the two crossed hurdle after hurdle. They communicated by email—several thousands of them—as Spruck spent sleepless nights on his couch with a pad of paper. Reaching a happy conclusion was far from a given. At one major stumbling block consisting of things called "level sets" and "branching snowflakes," they finally prevailed on the strength of a theorem from a completely different branch of math.

"This was quite emotionally difficult," Spruck says. "We died a thousand times and then lived. You have the feeling that the gods saved you somehow."

This process of idea-conjecture-idea-proof reflects the typical unfolding of progress in math. People have insights about a certain problem, and while there's not enough evidence to prove it, they formulate what they believe to be true. They share it and get immediate feedback from a large community of other mathematicians who challenge one another and hone the idea. "That's why things move so fast in math as compared to other fields," Spruck points out.

Then, whether weeks or decades later, someone else proves the conjecture, which then becomes a theorem. The community jumps on that new body of knowledge as well, applying it to their own specialties. The names of the conjecturers and provers remain permanently attached to their findings.

Will this be what Spruck and Ghomi are remembered for 100 years from now? "It might become the thing. I'm really happy with this," Spruck allows.

For all its concreteness once it reaches the stage of a proof, the process of math remains remarkably mysterious. Spruck says he usually starts with some intuition about a problem. He begins doodling as a way of focusing his mind, then ideas gradually begin to surface that his subconscious has been working on, and then he has to figure out how to make them tangible. "Students have terrible difficulty with that part: 'What do I write down?'" Spruck says.

For Spruck, doing math is similar to painting—he experiences both as a form of meditation. Two of his own canvases adorn his office.

"You get in a certain space," he says. "When you're really thinking about things, it's like being in a meditative state. Hours and hours go by and you don't even realize it.

"You take a blank canvas, you have certain fundamental rules, but it's all open. And the other thing that's like with painting, or anything else, is to love the challenges. It's not whether you succeed in the moment; it's to love the process of being lost in it."